西宮の家庭教師ダイアログによる過去問解説。今回は須磨学園中学校の過去問です。
(本年の過去問は、学校による公開は終了しています。 )
もくじ
1 計算問題
解説は省略します。
2 小問集合
解説は省略します。
3 旅人算とダイヤグラム

「旅人算とダイヤグラム」についての問題です。具体的な距離や速さの数値がなくても解けるタイプの問題です。距離のかわりに、\frac{1}{10}周などを一つの単位に用いて考えることがポイントです。
まずA、Bそれぞれの速さについて整理すると、
Aは休憩なしだと10分で1周するので、毎分\frac{1}{10}周と表せます。
Bは休憩なしだと20分で1周するので、毎分\frac{1}{20}周と表せます。
また、休憩ありだとAは15分で1周、Bは25分で1周しています。よって、AとBが同時にPを出発してから75分後に、また同時にPを出発することが分かります。
よって、下図のように75分以降のダイヤグラムは0分からの繰り返しとなります。

(1)難易度:★☆☆☆☆
ダイヤグラムから、50分までに線の交わった場所を数えると、5カ所(0分は数えない)なので出会った回数は5回です。
(2)難易度:★★★☆☆
ダイヤグラムを見ると3回目に出会ったのは25分と30分の間で、25分の時点でAとBは\frac{1}{2}周ぶん離れています。この後、ABが向かい合って進むので、3回目に出会うのは
25+\frac{1}{2}÷( \frac{1}{10}+\frac{1}{20})=28\frac{1}{3}(分)=28分20秒
(3)難易度:★★★★☆
ダイヤグラムを見ると、75分にAとBが同時にPを出発したとき、8回目に出会っていることになります。よって、10回目に出会う時間は2回目に出会う時間を求め、75分を加えればよいことが分かります。
2回目に出会ったのは15分と20分の間で、15分の時点でAとBは\frac{1}{4}周ぶん離れています。この後、ABが向かい合って進むので、2回目に出会うのは
15+\frac{1}{4}÷( \frac{1}{10}+\frac{1}{20})=16\frac{2}{3}(分)=16分40秒
よって、10回目に出会うのは、
75+16\frac{2}{3}= 91\frac{2}{3}(分)=91分40秒
(4)難易度:★★★★☆
AとBが逆向きに進んでいたときと同じく、同じ方向に進む場合もAとBが同時にPを出発してから75分後に、また同時にPを出発します。

ダイヤグラムを見ると、10分にAがBに追いついていることが分かります。また、75分のあとは同じグラフが繰り返され、1周期ごとに1回追いつくので、3回目に出会うのは、
75+75+10=160(分)
解答らんに合わせて160分00秒
4 立体の切断と体積

「立体の切断と体積」に関する問題です。立法体の切断じたいはシンプルなのですが、四面体がどう切られるかを考えるのは少し難しいかもしれません。
(1)難易度:★☆☆☆☆
四面体ACFHは立方体ABCD-EFGHから、すみっこにある三角すいを4つ切り取ったものです。
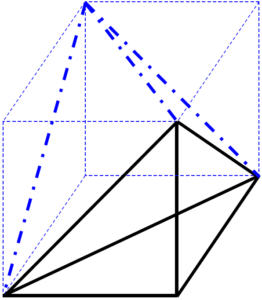
たとえば、上記の黒実線の三角すいCFGHの体積は、
6×6×\frac{1}{2}×6×\frac{1}{3}=36(㎤)
よって四面体ACFHの体積は、
6×6×6-36×4=72(㎤)
(2)難易度:★★★☆☆
点J、K、Lを通る平面で切ると、切断面は三角形となります。この頂点を下図のようにそれぞれ点O、P、Qとします。

切断したときにできる小さい方の立体は四面体ACFHと相似な四面体です。立方体の1面である正方形BCGFを取り出すと、下図のようになります。

正方形の対角線は真ん中で交わりますので、CP:CF=1:4となり、同じように考えて、CQ:CA=CO:CH=1:4となります。
よって、四面体CJKLの体積は、
72×\frac{1}{4}×\frac{1}{4}×\frac{1}{4}=\frac{9}{8}(㎤)
大きい方の立体の体積は、
72ー\frac{9}{8}=70\frac{7}{8}
(3)難易度:★★★★☆
点J、K、Lを通る平面で切ると、切断面は三角形となります。この頂点を下図のようにそれぞれ点Q、R、Sとします。
このような断面をかくときは、以下のルールに従います。
①まず同じ平面上にある点を結ぶ
②その直線を延長し、立体の辺の延長と交わる点をマークする
③平行な面にある断面の辺どうしは平行になる

(2)と同様に考えて、点Q、R、Sは、それぞれ
AS:AF=AQ:AC=AR:AH=3:4となるような位置にあります。
よって、四面体ASTRの体積は、
72×\frac{3}{4}×\frac{3}{4}×\frac{3}{4}=\frac{243}{8}(㎤)
大きい方の立体の体積は、
72-\frac{243}{8}=41\frac{5}{8}(㎤)
(4)難易度:★★★★☆
点J、K、Lを通る平面で切ると、切断面は三角形となります。この頂点を下図のようにそれぞれ点Q、T、Uとします。

ここで、正方形ADHEのある面を取り出します。直線JKと辺ADの延長との交わる点をVとし、直線VNと辺DHの交わる点をWとします。するとDV=CJなので、AD:DV=2:1
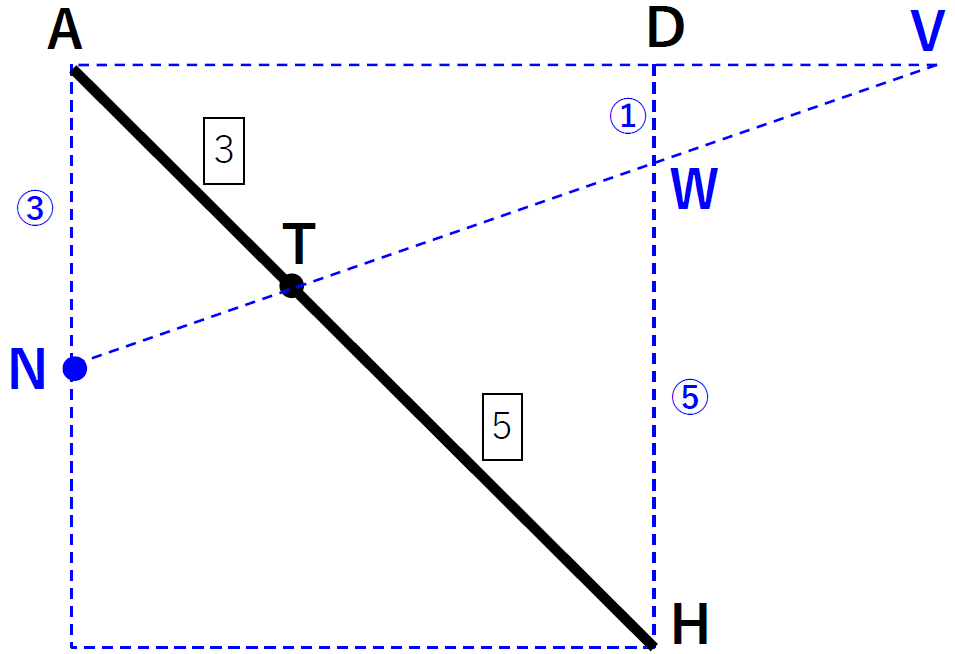
△VDWと△VANは相似なので、DW:AN=VD:VA=1:3
DW:DH=DW:AN×2=1:6だから、DW:HW=1:5
よって、AN:HW=3:5
△TANと△THWも相似なので、TA:TH=AN:HW=3:5
だから、AT:AH=3:8
同じように考えて、AU:AF=3:8
よって、四面体AQTUの体積は、
72×\frac{3}{4}×\frac{3}{8}×\frac{3}{8}=\frac{243}{32}(㎤)
大きい方の立体の体積は、
72-\frac{243}{32}=64\frac{13}{32}(㎤)
5 玉の分け方

「玉の分け方」に関する問題です。箱に入る玉の数の樹形図を正確にかき、重複と漏れのないように数えることが大事です。また、(3)(4)は設問の条件を正確に読み取る読解力が問われます。
(1)難易度:★★★☆☆
1番多くの玉が入っている箱に何個入っているかで整理し、樹形図にして数えます。

以上より、1+1+2+3+5+6+7+4+1=30通り
(2)難易度:★★★☆☆
上の樹形図から「玉の入っている箱について、各箱の中に入っている玉の個数がどの2つの箱についても異なる入れ方」つまり玉の個数が全部異なる入れ方をピックアップすると下図の赤字で、合計8通りとなります。

(3)難易度:★★☆☆☆
「同じ個数の玉が入っている2つの箱の中身を1つの箱にまとめる」ので…
(5,1,1,1,1)は1回目の【操作】で(5,2,2)となり、2回目の【操作】で(5,4)となります。
(4)難易度:★★☆☆☆
【操作】を逆にすると、偶数はその\frac{1}{2}の数2つに分かれます。
よって(4,3,2)は1回目の【逆操作】で(2,2,3,1,1)で順序を整理すると(3,2,2,1,1)となり、2回目の【逆操作】で(3,1,1,1,1,1,1)となります。
.png)


