西宮の家庭教師ダイアログによる過去問解説。今回は須磨学園中学校の過去問です。
もくじ
1 皮ふと血管

「皮ふと血管」に関する問題です。かなりの受験生が満点を取ったと思われる、非常に簡単な問題ばかりです。ミスをしないよう気をつけましょう。
問1 難易度:★☆☆☆☆
血液中に含まれ、病原体を排除する役割をもつのは白血球です。
問2 難易度:★★☆☆☆
問題文に「毛細血管を含む真皮の層」とあります。この生徒は紙で手を切ったものの血液が出なかったので、傷は真皮までいたらず、表皮のみを切ったと判断したと考えられます。
問3 難易度:★☆☆☆☆
場所ごとに表皮のつくられる速さ(1日あたり)を計算すると、
まぶた 0.07÷28=0.0025(mm/日)
手のひら 0.75÷50=0.015(mm/日)
足の裏 1.50÷50=0.03(mm/日)
よって、手のひらはまぶたの6倍、手のひらは足の裏の0.5倍となります。
問4 難易度:★☆☆☆☆
「セミやトンボ」「皮がはがれおちる」から連想されるのは脱皮ですね。
問5 難易度:★☆☆☆☆
「立毛筋」という名前からして、収縮したときに毛が立っているものを選ぶことになります。また、熱が外気に逃げると温度が下がるので、熱が逃げていないものを選びます。よって、①が正解です。
問6 難易度:★★☆☆☆
(ウ)(エ)(オ)寒いとき,指先の色は白っぽくなります。これは、皮ふ近くの血管が細くなることで、指先に流れる血液が少なくなるからです。
2 中和反応

「中和反応」に関する問題です。計算量も多くなく、この分野の問題としては易~標準的なレベルです。情報整理をきっちりおこなって取り組みましょう。
問1 難易度:★★☆☆☆
固体の水酸化ナトリウムの性質として、空気中の水蒸気を吸収してしまう、というものがあります。水蒸気を吸収すると、そのぶん重くなってしまいますので、正確に測ることにあまり意味がないのです。
【解答例】
空気中の水蒸気を吸収して重くなってしまうので、正確な重さが測れないから。
問2 難易度:★★☆☆☆
実験1では水酸化ナトリウム水溶液と塩酸をもちいて中和しているので、その結果できる白い固体は食塩です。
食塩の性質として正しいのは、「水100gにとける最大量は、水の温度を変えても大きくは増えない」「水にとかすと、その水よう液は電気を通す」の二つです。
問3 難易度:★☆☆☆☆
フェノールフタレインよう液は、アルカリ性で赤色、中性・酸性では無色となります。
実験1では水酸化ナトリウム水溶液に塩酸を加えていっているので、アルカリ性→中性→酸性と変化するはずです。
よって、(ア)は赤色、(イ)は無色であるとわかります。
問4 難易度:★☆☆☆☆
塩酸は、水に塩化水素という気体がとけてできています。よって塩酸を加熱して水を蒸発させると、塩化水素も一緒に気体となってとんでいってしまいます。
【解答例】
何も残らない
問5 難易度:★★☆☆☆
色が赤色から無色に変化したのは、塩酸を40mL加えたところです。よってその後加えたぶんの塩酸は、中和には関係せず、塩酸として存在しています。問4の結果からも分かるように、多く加えたぶんの塩酸は蒸発にともなってなくなってしまいます。
よって、蒸発皿に残る個体は11.7gのままです。
問6 難易度:★★★☆☆
表2より、塩酸を加えて中和させると、塩酸10mLあたり固体は1gずつ増えていくことが分かります。
また、Dをみると、30mL加えたところで10.8gであり、これが塩酸を増やすことで11.7gまで0増加します。つまり、0.9g増加したところまで塩酸を加えるとちょうど中和、つまり中性になります。
塩酸10mLあたり固体1g増えていたので、Dの状態から塩酸9mLを加えればあと0.9g増えますね。
よって、加える塩酸の合計は39mLとなります。
問7 難易度:★★★☆☆
まずはしっかりと情報を整理しましょう。
表2より、水酸化ナトリウム水溶液10mLには7.8g含まれていることが分かります。そして、これが39mLの塩酸と中和すると11.7gの食塩になります。
実験2のビーカーCでは、塩酸20mLを加えています。まだ中和は終わっていないので、加えた塩酸はすべて中和にかかわっています。中和によってできた食塩の重さは、
11.7×\frac{20}{39}=6(g)
3 光の性質

「光の性質」に関する問題です。問4~6は「アクリル板を何度も反射しながら通過する光」をあつかっており、少し難易度が高いです。
問1 難易度:★☆☆☆☆

実際に図中に線をかきこんで確認しましょう。下図の通り、ろうそくの炎が見えないのは③と④だと分かります。
問2 難易度:★☆☆☆☆
上図から分かるように、①、②で炎を見ることができるのは、光が直進するからです。
問3 難易度:★★★☆☆
図の右側に空白があることに注目して、鏡に反射したときに見える像をかきこんでいきます。さらに2回反射したときに見える像もかきます。そして、それぞれの炎の点を観測点と結びます。
1回反射の像は鏡と1回交差しているもの、2回反射の像は鏡と2回交差しているものが見えていることになります。



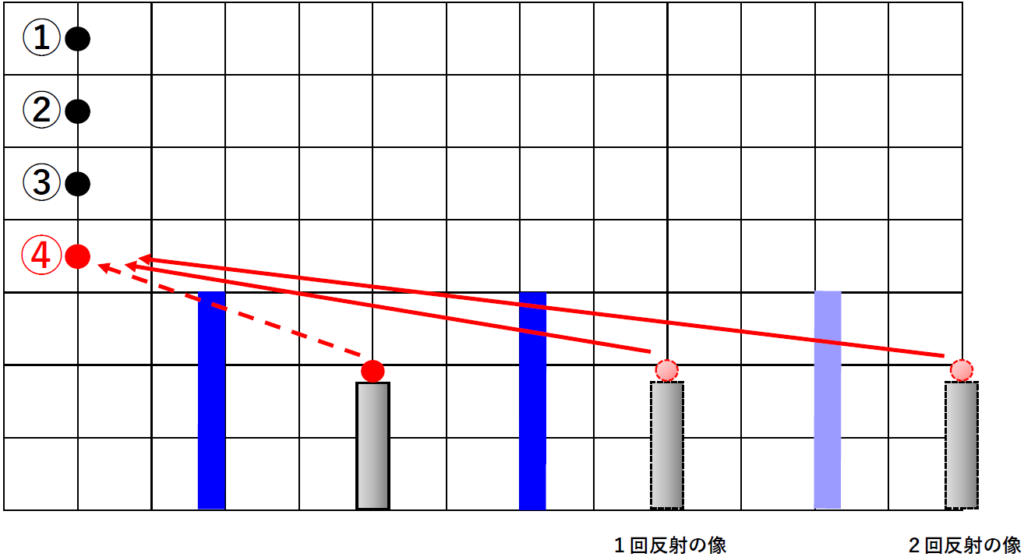
上図の通り、①からは本物の炎が、②と③からは本物の炎と1回反射の像が、④からは1回反射の像と2回反射の像が見えることになります。
問4 難易度:★★☆☆☆
本文に『炎の明るさは「ろうそくの炎から出て左のアクリル板を透過した光」と「ろうそくの炎から出て右のアクリル板に1回反射してから左のアクリル板を透過した光」の2つの明るさを足し合わせたもの』とあります。
もともとの炎の光の量を1とすると、「ろうそくの炎から出て左のアクリル板を透過した光」は、
1×\frac{4}{5}=\frac{4}{5}
また、「ろうそくの炎から出て右のアクリル板に1回反射してから左のアクリル板を透過した光」は、
1×\frac{1}{5}×\frac{4}{5}=\frac{4}{25}
よって、観察できる炎の明るさは、
\frac{4}{5}+\frac{4}{25}= \frac{24}{25}
問5 難易度:★★★☆☆
まず、ろうそくから観測者側に向かった光は1回も反射せず手前のアクリル板を通過(0回)、手前のアクリル板に反射したあと向こう側のアクリル板に反射して手前のアクリル板を通過(2回)、…と偶数回反射して観測者に届きます。
また、ろうそくから観測者の反対側に向かった光は反対側のアクリル板に反射して手前のアクリル板を通過(1回)、反対側のアクリル板に反射したあと手前のアクリル板に反射し、また反対側のアクリル板に反射して手前のアクリル板を通過(3回)…と奇数回反射して観測者に届きます。
よって、0回反射、1回反射以外にも2回、3回、4回…反射して観測者に届く光があります。
問6 難易度:★★★☆☆
ろうそくから観測者側に向かいアクリル板にあたった光のうち、\frac{4}{5}が通過し、\frac{1}{5}が反射します。このことから、アクリル板にあたっても光の合計は減らない(つまり吸収されたり散乱しない)ことが分かります。つまり、反射した光はその後何回か反射を繰り返すとしても、いずれ観測者側か反対側のどちらかに通過します。これはろうそくから観測者の反対側に向かう光についても同様です。
また、アクリル板を通過してくる光の足し合わせた量についても、観測者側と反対側とでは条件は同じだと考えられます。
以上より、ろうそくから観測者側に向かう光と反対側に向かう光をそれぞれ1とすると、その和が両側に等しく分配されて通過すると考えられるので、観測者側に通過する光は、
(1+1)÷2=1
よって、反射した後に通過した光の明るさもすべて足し合わせた炎の明るさは,もとのろうそくの炎の明るさの1倍であると分かります。
4 太陽と惑星の見え方

「太陽と惑星の見え方」に関する問題です。 \frac{(天体の直径)}{(観測位置からの距離)}で天体の見かけの大きさを計算するというところは少し発展的です。この設問を回答できるかが合否の一つの分かれ目になるかもしれません。
問1 難易度:★☆☆☆☆
(ア)月では地球上と比べて重力が小さくなります。
(イ) 重い天体ほど天体上にある物体にはたらく重力の大きさが大きくなります。太陽系の惑星の中では木星が一番重い惑星なので、木星における物体にはたらく重力の大きさが一番大きくなります。
(ウ)ブラックホールが暗いのは、光を吸いこむほど重力が大きいためです。このことから、ブラックホールは地球などの太陽系の天体よりも重いことが分かります。
問2 難易度:★☆☆☆☆
本文より、「陰」は「光が 物体にあたったときに、物体の反対側が暗く見える」こと、「影」は「光がさえぎられることで暗くなる」ことです。
よって、 ①スクリーン上に映る手のかげ、 ②晴れた日に涼むために入る木のかげ、それに⑤月食が「影」であることが分かります。
問3 難易度:★☆☆☆☆
日食は月が太陽と地球の間にあるとき、つまり「太陽、月、地球」の順に並んだときに太陽が月の「かげ」で見えなくなりま す。
問4 難易度:★★☆☆☆

問題を解く前に、なぜ\frac{(天体の直径)}{(観測位置からの距離)}で見かけの大きさが計算できるのか考えてみましょう。月と太陽の見かけの大きさが等しいということは、観測する人の視野の中での「角度」が等しいということです。下図のように観測者と月、太陽の上下の両端を結んで二等辺三角形をつくると、2つの三角形は相似であることが分かります。

\frac{(天体の直径)}{(観測位置からの距離)}は、これらの三角形における\frac{(三角形の底辺)}{(三角形の高さ)}にあたります。これは相似な三角形では等しくなりますね。
さらに、見かけの大きさが大きいと視野の中での「角度」が大きくなり、\frac{(天体の直径)}{(観測位置からの距離)}も大きくなるということです。
逆に、見かけの大きさが小さいと視野の中での「角度」が小さく、\frac{(天体の直径)}{(観測位置からの距離)}も小さくなります。
太陽と地球の距離が1億5000万km、月と地球の距離が38万kmとすると、これらの距離は両方とも三角形の「高さ」にあたりますので、三角形の相似比は、
150000000:380000=7500:19となります。
太陽、月の直径はこれらの三角形の「底辺」にあたるので、相似比をもちいて、
7500÷19=394.73…≒395(倍)
問5 難易度:★★☆☆☆
問4で求めた相似比を用いて、
3500×\frac{7500}{19}=1381578…≒138万(km)
問6 難易度:★★★☆☆
火星から見た太陽、フォボスそれぞれについて\frac{(天体の直径)}{(観測位置からの距離)}を計算すると、
火星から見た太陽: \frac{138万(km)}{2億7900万(km)}=\frac{23}{4650}
火星から見たフォボス: \frac{20(km)}{9380(km)}= \frac{1}{469}
よって、火星から見た太陽の見た目の大きさがフォボスの何倍かを計算すると、
\frac{23}{4650}÷ \frac{1}{469}≒2.3(倍)
これに合う見た目の大きさの図は②であると分かります。
.png)


