西宮の家庭教師ダイアログによる過去問解説。今回は兵庫県公立高校入試の過去問です。
西宮市立西宮高校、西宮東高校、神戸高校などの難関公立高校をめざすには、ぜひ全問正解したい問題です。
もくじ
1 小問集合
解説は省略します。
2 速度とグラフ

速さを使った連立方程式の問題です。昨年度と同じパターンの出題ですね。
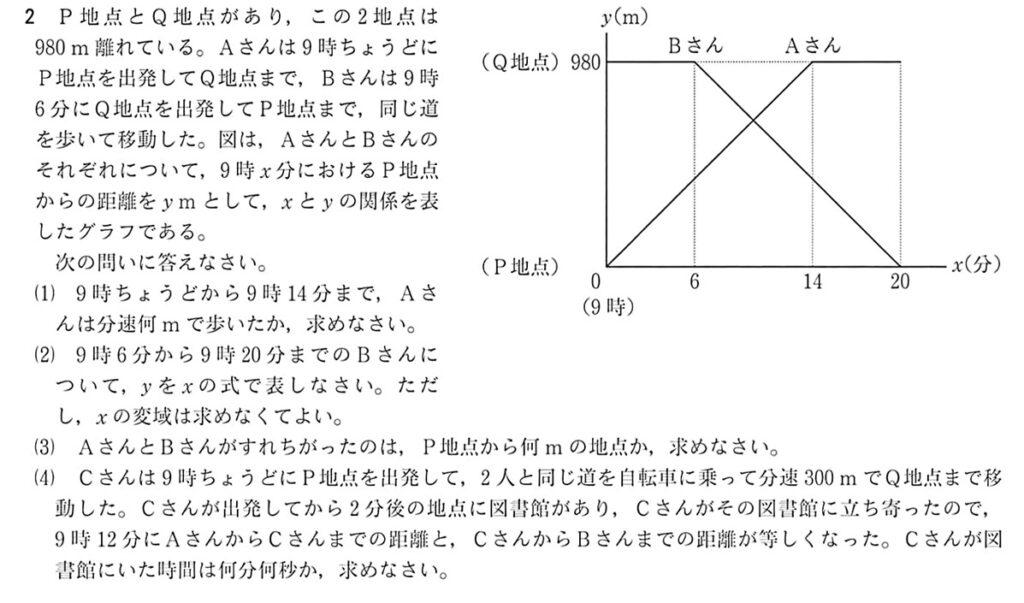
(兵庫県教育委員会の許可を得て掲載しています)
(1)難易度:★☆☆☆☆
Aさんは14分でP地点からQ地点についているから、
980÷14=70(m/分)
(2)難易度:★☆☆☆☆
9時6分と9時20分におけるBさんの位置と時刻の関係をグラフ上の座標(x,y)で表すと、
Q地点 → (6,980)…① P地点 → (20,0)…②
xとyの関係をy=ax+bとおく。
①を代入して、980=6a+b …③
②を代入して、0=20a+b よって、b=-20a
これを③に代入して、980=-14a ゆえに、a=-70、b=1400
よって、求める式は、y=-70x+1400
(3)難易度:★★☆☆☆
(2)と同様に、9時0分と9時14分におけるAさんについて、xとyの関係を表してみましょう。Aさんの場合は…
P地点 → (0,0) Q地点 → (14,980)
なので、Aさんについてxとyの関係はy=70x
AさんとBさんがすれちがうことは、つまりAさんとBさんが同じ時刻に同じ位置にいることなので、
y=70x …④
y=-70x+1400…⑤
④と⑤を同時に満たすxとyを求めればよいことになります。つまり連立方程式を解くということです。
④-⑤より、0=140x-1400 ゆえにx=10、y=700
よって、AさんとBさんがすれ違ったのは、P地点から700mのところ。
(4)難易度:★★☆☆☆
「9時12分、AさんとCさんまでの距離とCさんからBさんまでの距離が等しくなった」とあります。ここでAさんとBさんの歩く速さが70m/分で等しいことに注目します。
歩く速さの等しいAさんとBさんがすれちがったあと、AさんとCさんまでの距離とCさんからBさんまでの距離が等しくなった。これは、「CさんはAさんとBさんがすれちがった2分後 、AさんとBさんがすれ違った地点にいる」ということです。
グラフをかいて考えましょう。(本番は問題の図にかきこみましょう)

こういうことですね。そして、Cさんは分速300mの自転車で移動しているのでこの場所に到着するには、
700÷300=\frac{7}{3}(分)
つまり2分20秒かかることになります。実際には、12分後にこの地点にいるので、図書館に立ち寄っていた時間は
12分 - 2分20秒 = 9分40秒
3 平面図形

平面図形の問題です。これも昨年度のパターンですね。
(4)は適切な補助線を引けるかどうかがカギです。

(兵庫県教育委員会の許可を得て掲載しています)
(1)難易度:★☆☆☆☆
基本的な証明問題ですね。誘導に乗るだけなので、基本問題をしっかり練習できていれば正解できるでしょう。
<証明>
△ACEと△ODEにおいて、
対頂角は等しいから、
∠AEC=∠OED…➀
仮定より、
AC//DO…②
平行線の錯角は等しいから、
②より、∠ACE=∠ODE…③
➀、③より、2組の角がそれぞれ等しいから、
△ACE∽△ODE
よって、(ⅰ)ウ(ⅱ)オ
(2)難易度:★☆☆☆☆
三平方の定理を使うだけですね。
線分ABは円Oの直径で、Cは円O上の点なので、∠ACB=90°
よって、三平方の定理より、AC²+BC²=AB²
AC=6、BC=8だから、BC²=64-36=28より、BC=2\scriptsize\sqrt{7}
(3)難易度:★★☆☆☆
方針としてはまず△ABCの面積を求め、底辺の比を用いて△ACEの面積を求めます。
△ACE=AB×AC÷2=6\scriptsize\sqrt{7} (㎠)
ここで、(1)で証明した相似を使います。
△ACE∽△ODEより、
AE:OE=AC:OD=3:2
よって、AE=\frac{3AO}{3+2}=\frac{12}{5}(㎝)
△ACE=△ABC× \frac{AE}{AB} =\frac{9\sqrt{7}}{5}
(4)難易度:★★★☆☆

補助線が必要なのはすぐ分かりそうですが…
DEを求めたい
↓
CDを求めれば比を使って計算できそう
↓
CDを辺にもつような直角三角形がかけないか?
と発想すればよいわけです。

点Oから線分BCに下した垂線の足をHとおきます。
このとき、△OBH≡△OCH(証明は省略します)だから、
CH=BH=BC× \frac{1}{2} = \scriptsize\sqrt{7}
△OCHにおいて、三平方の定理より
OH²=OC²-CH²16-7=9より、
OH=3
また、OH//ACだから、点D、O、Hは一直線上にあり、
DH=DO+OH=7
△CDHにおいて、
三平方の定理よりCD²=CH²+DH²=7+49=56より、
CD=2\scriptsize\sqrt{14}
△ACE∽△ODEより、
CE:DE=3:2だから、
DE=\frac{2CD}{3+2}=\frac{4\sqrt{14}}{5}(㎝)
4 2次関数と回転体


(兵庫県教育委員会の許可を得て掲載しています)

関数と回転体の問題ですね。
(1)難易度:★☆☆☆☆
y=\frac{1}{2}x² …①
y=ax² …②
点Cは①上の点だから、y=\frac{1}{2}x²にx=2を代入して、
y=\frac{1}{2} × 4=2
(2)難易度:★☆☆☆☆
点Aは②を通るから、 y=ax² にx=2を代入して、y=4a
よって、A(2,4a)
点Bも②を通るから、 y=ax² にx=4を代入して、y=16a
よって、B(4,16a)
また、xの値が2から4まで増加するときの変化の割合が \frac{3}{2} なので、
\frac{16a-4a}{4-2} = \frac{3}{2}
これを解くと、a= \frac{1}{4}
(3)① 難易度:★★☆☆☆
(2)より、A(2,1)、B(4,4)
直線ABをあらわす式を求めるために、この式をy=bx+c とおきます。
b= \frac{4-1}{4-2} = \frac{3}{2}
y= \frac{3}{2}x+c がA(2,1)を通るから ,この式にx=2、y=1を代入して、
1=3+c ゆえに、c=-2
以上より、直線ABをあらわす式はy= \frac{3}{2}x-2
また、点Dはy軸に関してCと対称な点だから、D(-2,2)
よって、点Eのx座標は-2。
y= \frac{3}{2}x-2 にx=-2を代入すると、
y=-3-2=ー5
よって、E(ー2,-5)
(3)② 難易度:★★☆☆☆

四角形ACDEは上の図のようになり、
・AC//EDの台形
・∠C=∠D=90°
・AC=2-1=1 CD=2+2=4 DE=5+2=7
これを直線CDを軸に回転させると、横に倒した山のようになりますね。


この形(山型、プリン型)の体積は定番ですね。大きな円すいから小さな円すいを引くと体積が求められます。
大小それぞれの円すいの高さを求めるために平面に戻ります。

DCとEAの延長の交点をFとおくと、
CA//DEより、△FCA∽△FDE(証明は省略します)だから、
FC:FD=CA:DE=1:7なので、FC:FD:CD=1:7:6
CD=4㎝より、
FC=4× \frac{1}{6} = \frac{2}{3}
FD=4× \frac{7}{6} = \frac{14}{3}
よって求める体積は、
(大きな円すい)-(小さな円すい)
=7×7× π × \frac{14}{3} × \frac{1}{3} - 1×1× π × \frac{2}{3} × \frac{1}{3}
=76π (㎤)
5 確率と立体図形

(兵庫県教育委員会の許可を得て掲載しています)

確率と立体図形を組み合わせた問題ですね。複雑そうに見えますが、整理して考えることができれば意外とすんなり解けます。
(1)難易度:★☆☆☆☆
A、B、C、D、Eのカードが入っている袋を(あ)とし、B、C、Dのカードが入っている2つの袋をそれぞれ(い)、(う)と呼ぶことにします。
(あ)-(い)-(う)それぞれの袋から1枚ずつカードを選ぶので、
B-B-B、C-C-C、D-D-D
の3通り。
(2)① 難易度:★☆☆☆☆
BかCのどちらかが2枚、もう片方が1枚選ばれればよいので…
B2枚、C1枚になるのは、
B-B-C、B-C-B、C-B-Bの3通り。
B1枚、C2枚になるのは、
C-C-B、C-B-C、B-C-Cの3通り。
あわせて6通り。
(2)② 難易度:★★☆☆☆
図形Xが線分になる場合のうち、延長した直線が辺ABとねじれの位置(交わってもいないし、平行でもない)にあるのは、CD、CE、DEの3つ。
図形XがCDとなるのは、①と同様に数えられるので、6通り。
図形XがCEとなるのは、E-C-Cの1通り。
図形XがDEとなるのは、E-D-Dの1通り。
あわせて8通り。
(2)③ 難易度:★★☆☆☆
頂点を3つ選んだとき、面積が2㎠の三角形となるのは、△ABD、△ACE、△BCD、△BCE、△BDE、△CDEの6つです。

たとえば、△BCDなど正方形BCDEを対角線で切ったものは2㎠の直角二等辺三角形であることに気づきやすいですが、△ACEと△ABDもそれらと合同な直角三角形です。

このうち、図形Xの条件で△ACEはつくることができません。AとEのカードは(あ)の袋にしか入っていないので両方選ぶことはできないからです。
また、△ABD、△BCE、△BDE、△CDEについては、(あ)からAまたはEのカードをえらび、のこりの2枚のカードをそれぞれ(い)または(う)から選ぶことになるので、それぞれ2通りずつあります。
さらに、△BCDについては、(あ)、(い)、(う)のいずれかの袋からB、C、Dのカードを1枚ずつとる選び方なので、
3×2×1=6(通り)
以上より、2㎠の三角形となるカードの取り方は、2×4+6=14(通り)
すべてのカードの選び方は、5×3×3=45通りなので、
2㎠の三角形となる確率は、14÷45= \frac{14}{45}
6 資料の読み取り




(兵庫県教育委員会の許可を得て掲載しています)

資料の読み取りに関する問題ですね。内容の読み取りさえできれば、非常に簡単で、上位層を狙うなら確実に満点をとっておきたい。絶対に落とせない問題といえるでしょう。
(1)難易度:★☆☆☆☆
りょうさんが「各種目で同じ順位の選手がいなければ、それぞれの選手について、3種目の順位をかけ算してポイントを算出するんだ」と言っています。
よって、マウェム選手のポイントは、
3×2×7=42(ポイント)
(2)① 難易度:★☆☆☆☆
平均順位を表にかきこんでいってみましょう。
| 選手 | スピード | ボルダリング | リード | 平均 |
| ヒネス ロペス | 1 | 7 | 4 | 4 |
| コールマン | 6 | 1 | 5 | 4 |
| シューベルト | 7 | 5 | 1 | 4\frac{1}{3} |
| ナラサキ | 2 | 3 | 6 | 3\frac{2}{3} |
| マウェム | 3 | 2 | 7 | 4 |
| オンドラ | 4 | 6 | 2 | 4 |
| ダフィー | 5 | 4 | 3 | 4 |
すると、もっとも平均順位の値が小さいのは、ナラサキ選手で、 3\frac{2}{3}位であったことが分かります。
ナラサキ選手は本来の総合順位4位の選手です。
(2)② 難易度:★★☆☆☆
3種目とも10位だった場合、かけ算で出すポイントは1000。
3種目の順位が(10-n)位、10位、(10+n)位だった場合、かけ算で出すポイントは…
(10-n)×10×(10+n)=10(100-n²)
=1000-10n²
よって、そのポイント差は10n²
(2)③ 難易度:★★☆☆☆
0<n<10の範囲ですが、nは整数なので1≦n≦9と表すこともできます。
一方、ポイント差は10n²とあらわせるので、nの絶対値が大きいほどポイント差は大きくなります。よって、n=9のとき、ポイント差は最大になり
10×9²=810
(3)難易度:★★☆☆☆
20人の選手で大会を行っているので、順位の値は1以上20以下の整数です。
B選手の方が順位を決めやすいので、B選手から考えてみましょう。
B選手は15位の種目があるのでポイントは15の倍数です。15の倍数で401以上410未満という範囲を満たすのは405。よって、Bのポイントは405です。
さらに、B選手の15位以外の2種目の順位の積は、
405÷15=27=3³
なので、ほかの順位は3位と9位であることが分かります。
一方、A選手は4位の種目があるので、ポイントは4の倍数です。4の倍数で401以上410未満という範囲を満たすのは404と408。
このうち、404=4×101で、101は素数なので、1以上20以下の順位という条件に合いません。よって、Aのポイントは408に確定します。
ここで、A選手の4位以外の2種目の順位の積は、
408÷4=102=2×3×17
1以上20以下の順位という条件にあうように4位以外の順位を考えると、
6位と17位となります。
まとめると、
A選手の3種目の順位は、4位、6位、17位で408ポイント。
B選手の3種目の順位は、3位、9位、15位で405ポイント。
以上より、 A選手の方が下位で、残りの2種目の順位は6位と17位。
.png)


